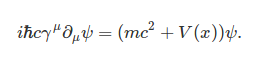Particles and Antiparticles, a mathematical difference.

The discovery of antiparticles was a revolutionary event in physics and now we are capable to produce and analyze antimatter.

We are usually told that the world of antiparticles is like an exact copy of ours but with some peculiarities. The lack of evidence of large quantities of antimatter in the observable universe is an indication that the symmetry between particles and antiparticles is not perfect. However, from a mathematical perspective it is possible to argue about a significant asymmetry between particles and antiparticles.

Group theory tell us that the Dirac spinor is a double cover representation of the Special Lorentz Group denoted by SO(1,3). This group has a subgroup characterized for maintaining the direction of time. As a result, the operations in this group can be visualized as either spatial rotations or boosts of velocity. In other words, this subgroup has a simple and intuitive interpretation and can be associated with particles. Therefore, antiparticles are the complement of the total group with the subgroup of particles. This mathematical construction is called coset. Consequently the world of pure particles has the structure of a group while the world of pure antiparticles has the structure of a coset!

This argument can be illustrated in the following diagram where O_{+}(1,3) is the group that maintains the direction of time.

The book that contains a detailed description of the group structure of spinors is

* Pertti Lounesto, Clifford Algebras and Spinors, Cambridge University Press, May 3, 2001

Bounded states in a linear potential

The Dirac equation with interaction in the mass is

In this case the potential does not correspond to an electric potential, nevertheless, it is often used in the literature. Something that may initially look surprising is the fact that this type of interaction supports bounded states for monotonically increasing potentials as shown in the figure below

This has been reported in the literature for sometime but without much of an explanation. The deeper insight came from the study of the Dirac equation in solid state physics where this type of system was recognized as the result of the contact of two topologically distinct phases: one with positive mass and the other one with negative mass. This contact gives origin to the so called zero mode states that have many interesting features and are the subject of intensive research today.

I published a generalization of this bounded state with additional nonlinear interactions in my recent paper at PRL

https://journals.aps.org/prl/accepted/14070Y2cTa61f86ba97d95a1f5d388e103887cbff

Relativistic electron in a strong laser field: Quantum spreading

Following the previous post about a relativistic classical particle in a laser field, here we have the quantum version where the center of the wavepacket still follows the classical trajectory.

This movie corresponds to a weak relativistic electron interacting with a laser field. The laser wavelength is 800 nm with an intensity of 10^20 W/m^2. The propagation follows the  z direction. The electric field is polarized along the x direction where the oscillation is observed.

As we can clearly see, the wavepacket spreading is significant even in a single oscillation!  Of course, this information is absent in the classical model.

A second animation is shown below for a stronger laser field

Relativistic classical electron in a laser field

A particle in a laser field with fixed direction and infinite wavefront has analytic solutions in both the quantum and classical realms.
These solutions allow for the possibility of electromagnectic wavepackets modulated in the direction of motion.
 
The quantum solution of the Dirac equation was found by Volkov in the early days of quantum mechanics!

Volkov D M 1935 Z. Physik 94, 250

Contrary to expectations, the classical solutions appeared much later. The following book contains a very complete analysis of the classical case

Electrodynamics: A Modern Geometric Approach (Progress in Mathematical Physics) by William E. Baylis, Birkhäuser; Corrected edition (January 12, 2004)

The trajectories for linear and circular polarization can be seen in the following movies:

Linear polarization

Circular polarization

An interactive Mathematica cdf document can be downloaded from
http://www.princeton.edu/~rcabrera/Volkov_LinearPolarization.cdf

The general theory is part of the lectures notes at
https://github.com/cabrer7/Lectures-On-Relativity

News: The case with linear polarization was published at the Wolfram Demonstrations Project:

Renan Cabrera"Classical Relativistic Particle in a Linearly Polarized Laser Field"
 http://demonstrations.wolfram.com/ClassicalRelativisticParticleInALinearlyPolarizedLaserField/
 Wolfram Demonstrations Project
 Published: September 15, 2017

Relativistic Dynamical Inversion RDI

Analytic solutions to coherent control of the Dirac equation and beyond  

My latest arxiv paper is online 

https://arxiv.org/abs/1705.02001

This work introduces Relativistic Dynamical Inversion (RDI) as a technique to find analytic solutions to the Dirac equation.

Update: This paper was just accepted to appear at Phys. Rev. Lett.

https://journals.aps.org/prl/accepted/14070Y2cTa61f86ba97d95a1f5d388e103887cbff

Ground state for a Dirac system confined by a combination of magnetic and electric fields.

 

A course on Relativity using Clifford (geometric) algebras in Mathematica

I am posting my lectures notes on Classical and Quantum Relativistic Mechanics at

https://github.com/cabrer7/Lectures-On-Relativity

I am preparing these notes in Mathematica, so, there are actual functions that perform symbolic and numerical calculations. If you do not have Mathematica, you can download the companion pdf documents or download the Mathematica CFD player for free at:

https://www.wolfram.com/cdf-player/

These lecture notes employ the language of Clifford algebras in two flavors: The Algebra of the Physical Space (APS) and the  Space Time Algebra (STA).

Contrary to the literature about Clifford algebras in physics, I decided to heavily rely on matrix representations. Clifford algebras can be developed from elegant axiomatic principles where no matrix is necessary at all. Nevertheless, I personally saw that most people claim to be too busy for that. My hope is that a direct exposure of the matrix representation will give them a more familiar environment based on simple standard linear algebra. 

 
Two snapshots of randoms pages