Thursday, February 23, 2012
Sunday, February 12, 2012
Conservation of Shannon information in classical mechanics
There are many places where to find the proof of the conservation of the quantum Shannon information under unitary evolution. However, I just could not find the equivalent proof that everybody talks in classical mechanics, so here it goes.
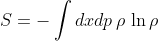
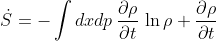
The Lioville equation can be expressed in terms of a self-adjoint operator as observed by Koopman and von Neumann, such that
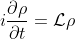
Given that the Liouvillian follows the Leibniz rule, which is true for conservative systems
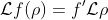
it is now easy to prove that
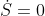
This fact is in complete contrast with respect to the thermodynamical entropy, which can be fundamentally irreversible.
-This entry was powered by http://www.codecogs.com/latex/eqneditor.php
The Lioville equation can be expressed in terms of a self-adjoint operator as observed by Koopman and von Neumann, such that
Given that the Liouvillian follows the Leibniz rule, which is true for conservative systems
it is now easy to prove that
This fact is in complete contrast with respect to the thermodynamical entropy, which can be fundamentally irreversible.
-This entry was powered by http://www.codecogs.com/latex/eqneditor.php
Thursday, February 9, 2012
DUST
DUST stands for Differential Unitary Space Time coding. This coding method is used in the transmission of information from multiple antennas to multiple antennas.
The transmission of information in a block can be modelled with the following equation

where S is the input matrix, H is the channel matrix, \rho is a scalar coefficient that modulates the channel and W is the noise.
DUST encodes the information in a unitary matrix U_n, which is indirectly encoded through a sequence of two S unitary blocks as
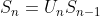
If H is full-rank and the channel does not change significantly in the time the two blocks are transmitted. The unitary matrix U can be recovered from the sequence of two received unitary blocks X without! the need to know the channel H as
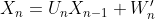
where the new noise is defined as

-This entry was powered by http://www.codecogs.com/latex/eqneditor.php
The transmission of information in a block can be modelled with the following equation
where S is the input matrix, H is the channel matrix, \rho is a scalar coefficient that modulates the channel and W is the noise.
DUST encodes the information in a unitary matrix U_n, which is indirectly encoded through a sequence of two S unitary blocks as
If H is full-rank and the channel does not change significantly in the time the two blocks are transmitted. The unitary matrix U can be recovered from the sequence of two received unitary blocks X without! the need to know the channel H as
where the new noise is defined as
-This entry was powered by http://www.codecogs.com/latex/eqneditor.php
Tuesday, February 7, 2012
Random Unitary Matrices
The generation of random unitary matrices has many applications in many fields.
The simplest method is based on the QR decomposition of a random complex matrix with independent elements following a Normal distribution.
In Mathematica one can generate a random complex number with Normal distribution for both the real and imaginary parts with the following function
NormalRandomComplex[] := (#[[1]] + #[[2]]*I) &@
RandomReal[MultinormalDistribution[{0, 0}, {{1, 0}, {0, 1}}]]
where {0, 0} specifies the origin and {{1, 0}, {0, 1}} the covariance matrix (standard deviation 1)
The function that generates the random n x n unitary matrix is
In this code, the QR decomposition of the complex random matrix with normal distribution outputs a unitary matrix "q" and a triangular matrix "r". The sought random unitary matrix is a correction of "q", which must be multiplied by a diagonal matrix filled with 1 and -1 according to the sign of the corresponding diagonal element of "r".
The simplest method is based on the QR decomposition of a random complex matrix with independent elements following a Normal distribution.
In Mathematica one can generate a random complex number with Normal distribution for both the real and imaginary parts with the following function
NormalRandomComplex[] := (#[[1]] + #[[2]]*I) &@
RandomReal[MultinormalDistribution[{0, 0}, {{1, 0}, {0, 1}}]]
where {0, 0} specifies the origin and {{1, 0}, {0, 1}} the covariance matrix (standard deviation 1)
The function that generates the random n x n unitary matrix is
RandomUnitaryMatrix[n_] := Module[{z, q, r},
z = Table[NormalRandomComplex[], {n}, {n}];
{q, r} = QRDecomposition[z];
q.DiagonalMatrix[Sign[Tr[r, List]]]
] z = Table[NormalRandomComplex[], {n}, {n}];
{q, r} = QRDecomposition[z];
q.DiagonalMatrix[Sign[Tr[r, List]]]
In this code, the QR decomposition of the complex random matrix with normal distribution outputs a unitary matrix "q" and a triangular matrix "r". The sought random unitary matrix is a correction of "q", which must be multiplied by a diagonal matrix filled with 1 and -1 according to the sign of the corresponding diagonal element of "r".
Subscribe to:
Posts (Atom)
