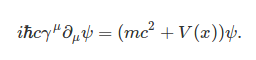Particles and Antiparticles, a mathematical difference.

The discovery of antiparticles was a revolutionary event in physics and now we are capable to produce and analyze antimatter.

We are usually told that the world of antiparticles is like an exact copy of ours but with some peculiarities. The lack of evidence of large quantities of antimatter in the observable universe is an indication that the symmetry between particles and antiparticles is not perfect. However, from a mathematical perspective it is possible to argue about a significant asymmetry between particles and antiparticles.

Group theory tell us that the Dirac spinor is a double cover representation of the Special Lorentz Group denoted by SO(1,3). This group has a subgroup characterized for maintaining the direction of time. As a result, the operations in this group can be visualized as either spatial rotations or boosts of velocity. In other words, this subgroup has a simple and intuitive interpretation and can be associated with particles. Therefore, antiparticles are the complement of the total group with the subgroup of particles. This mathematical construction is called coset. Consequently the world of pure particles has the structure of a group while the world of pure antiparticles has the structure of a coset!

This argument can be illustrated in the following diagram where O_{+}(1,3) is the group that maintains the direction of time.

The book that contains a detailed description of the group structure of spinors is

* Pertti Lounesto, Clifford Algebras and Spinors, Cambridge University Press, May 3, 2001

Bounded states in a linear potential

The Dirac equation with interaction in the mass is

In this case the potential does not correspond to an electric potential, nevertheless, it is often used in the literature. Something that may initially look surprising is the fact that this type of interaction supports bounded states for monotonically increasing potentials as shown in the figure below

This has been reported in the literature for sometime but without much of an explanation. The deeper insight came from the study of the Dirac equation in solid state physics where this type of system was recognized as the result of the contact of two topologically distinct phases: one with positive mass and the other one with negative mass. This contact gives origin to the so called zero mode states that have many interesting features and are the subject of intensive research today.

I published a generalization of this bounded state with additional nonlinear interactions in my recent paper at PRL

https://journals.aps.org/prl/accepted/14070Y2cTa61f86ba97d95a1f5d388e103887cbff